TRADERS´ES 09

23 / 78

23
PERSPECTIVAS
TRADERS´ 09.2018
refleja que aproximadamente en un año determinado el
80% de los day traders perdieron dinero neto y el 20% lo
ganaron y así sucede con bastante precisión cada año,
con lo que cabría esperar que solo gane aproximada-
mente el 20% del 20% al año siguiente, ya que muchos de
los ganadores perderán al año siguiente. Eso sí, el estudio
demuestra que a la larga puede haber un reducido grupo
de expertos intradía o ganadores consistentes, ya que el
porcentaje de ganadores en dos años diferentes es del
20% y 19,5%, lo que daría una esperanza matemática de
3,9% de ganadores (20% x 19,5%). Sin embargo el resul-
tado del estudio da un porcentaje de ganadores consis-
tentes que ganan en un año y también en el año previo
del 6,6%, por encima del 3,9% que arrojaría la expectativa
estadística, si no existiera consistencia en un pequeño
grupo de ganadores. A largo plazo todos los estudios que
he estudiado muestran un porcentaje alrededor del 80%
en un año dado y a largo plazo cercano al 1% (ganador
consistente durante años, ya que el que gana 2 años
seguidos puede pasar a ser perdedor neto en el tercero).
La regla del 72
Con esa sencilla fórmula lograremos calcular de manera
rápida cuantos años necesitaríamos aproximadamente
para doblar la inversión. Es una manera cómoda y eficaz
de cálculo de los años necesarios para doblar el capital
sin necesidad de calculadora.
Años necesarios para doblar una inversión a “x” tasa de
rentabilidad:
= 72 / r (tasa de rentabilidad)
Podríamos calcular sabiendo la rentabilidad anual,
cuantos años tardaríamos en doblar el capital. Por
ejemplo, logrando una rentabilidad anual del 9% tarda-
ríamos 8 años en doblar el capital.
Tasa de rentabilidad necesaria para doblar la inversión a
“x” años:
= 72 / n (número de años)
Dándole la vuelta, podemos calcular cuantos años nece-
sitaríamos para doblar el capital aplicando cualquier tasa
de rentabilidad.
• El número 72 es elegido como el numerador más
práctico, ya que tiene muchos pequeños divisores
como el 1, 2, 3, 4, 6, 8, 9,12 y 18.
• Da una muy buena aproximación para una tasa anual
de rendimiento entre el 4.9% al 11%.
• La regla del 69 sería más precisa, para un resultado
entre 0% a 0.5%.
• La regla del 70 sería más precisa para un resultado
entre 0.5% al 5%.
• Si utilizas esta fórmula en tasas de rendimiento altas,
la estimación aproximada se vuelve menos precisa
Ganando un 7% de rentabilidad anual tardaríamos aproxi-
madamente 10 años en duplicar nuestro capital. Ganando
un 10% tardaríamos aproximadamente unos 7,3 años en
doblar la inversión.
Aplicado al crecimiento del PIB de un país, si tu país crece
al 4% anual, tardará 18 años en doblar el PIB. Y cuidado
si tu país tiene una inflación galopante del 12%, en solo 6
años a esa tasa inflacionaria tu dinero perderá la mitad
de su valor.
Imagina ahora uno de esos préstamos, que rozan la usura,
con los cuales miles de españolitos de a pié se hipotecan
o endeudan para irse de vacaciones, comprar un coche
o electrodomésticos. De esos préstamos rápidos y caros
que anuncian por la televisión. Imagina que los intereses
fueran de un 18%. Pues podemos aplicar la regla del 72.
72/18% = 4 años. Si el préstamo fuera a 4 años, en 4 años
pagaríamos el doble de la cuantía del préstamo. Cuidado
con la otra cara del interés compuesto, que aparece en
los intereses de las deudas. Haz que el interés compuesto
trabaje para ti y no al revés.
Le voy a poner un ejemplo de una inversión de largo plazo
en la que el precio de la acción evoluciona de forma muy
satisfactoria:
Imagine que compra 10.000 títulos de una acción que
cotiza a 1 euro. Es decir invierte 10.000€.
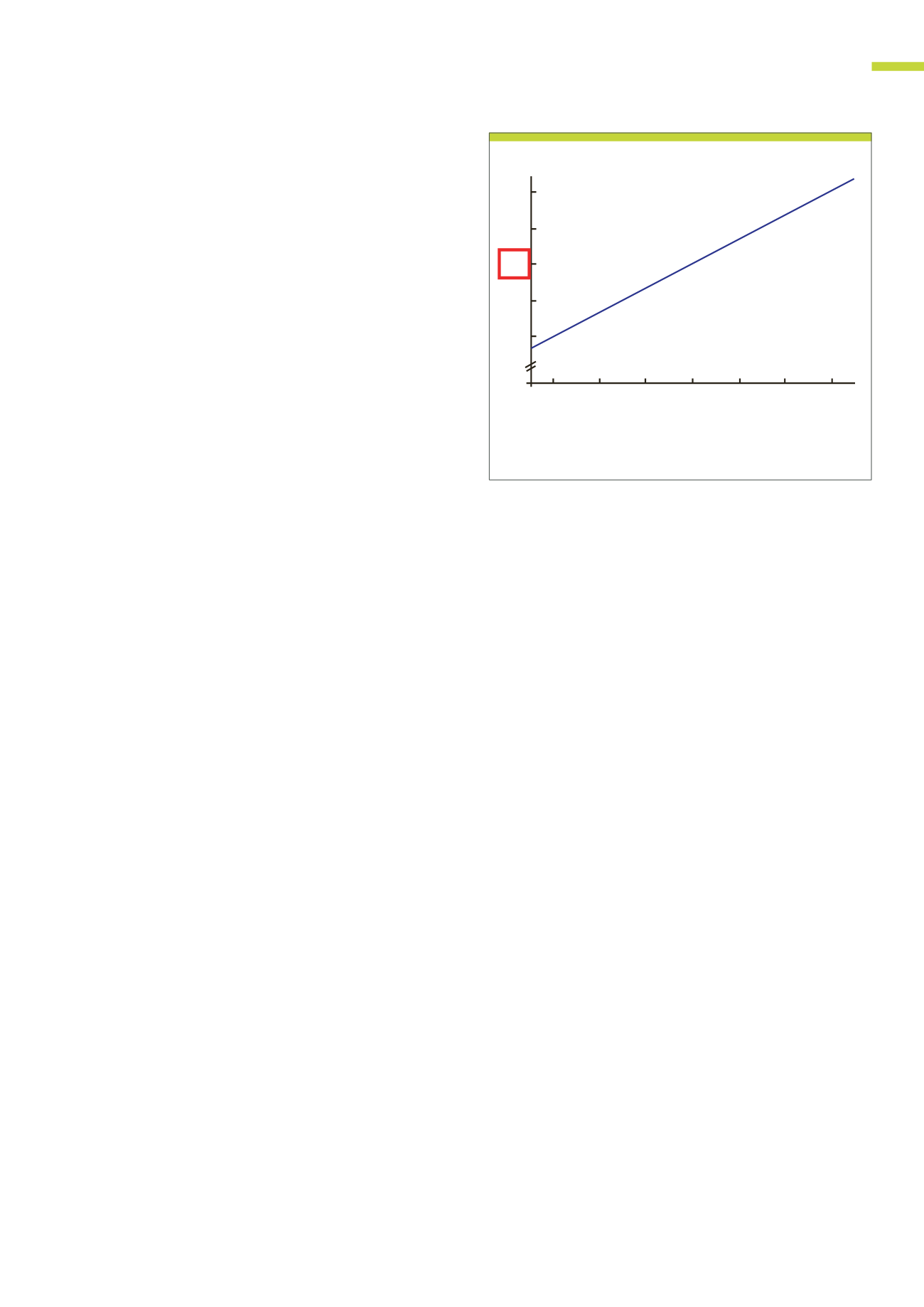
En este gráfico veríamos la desviación según la tasa de rentabilidad y vemos
como la regla del 72 funcionaría muy bien con una rentabilidad en la zona
central entre el 5% y el 11% aprox.
Fuente:
G2 Desviación según la tasa de rentabilidad
74
73
72
71
70
69
0.02 0.04 0.06 0.08 0.10 0.12 0.14